冊子「啓林」高数編（啓林館）1994年6月号

「回れ、ゴンドラ」、ロビンフッドとレスキュー隊
一般角の正弦・余弦の導入

広　瀬　　徹

　1月24日、1年4組、90ﾟ以上の三角比の導入を、コンピュータを使った自作のゲーム風ドリルＣＡＩ「回れ、ゴンドラ」で授業をしました。
　前の時間に、終わり5分前
　　　　sin 120ﾟ＝？
と書いて、「120ﾟの直角三角形なんて作れないけど、人間はそれを考え出してしまうんです。その授業をコンピュータでします。」と、予告してあります。

　学期にいっぺんぐらいしかコンピュータをさわりませんから、生徒たちはニコニコしてコンピュータ室にやってきます。
　スイッチ・オン。起動画面は、阪神パークの回転ゴンドラの写真です。

図1　「回れ、ゴンドラ」起動画面

　鋭角の三角比の説明のあと、鈍角の三角比が、半径1の円周上の点の座標と関連して、ｙそのものの値が sinθ となり、ｘそのものの値が　cosθ となることを示します。

　そうはいっても画面での説明表示ぐらいでそう分かるはずがありません。
　ロビンフッドの登場です。
　乱数を使って角度を、-300ﾟから 400ﾟまでひとつ決めて、たとえば
　　　　sin 160ﾟ＝？
と問題を出します。
　　　　sin 160ﾟ＝ sin 20ﾟ
とつかんだ生徒は、持ってきた教科書の表から 　　　　sin 20ﾟ＝ 0.3420
を見つけだして入力します。
　するとｙ軸上の 0.3420 の位置に赤い的が現れます。
　ロビンフッドがゴンドラに乗り込むと、ゴンドラが回り始めます。
　160ﾟまでくると、止まります。そしてそのゴンドラの高さから細い線（ロビンフッドの矢）が飛び出てきます。
　スーッとすいこまれるように、設定した的に当たるとき、思わず生徒たちは、当たれ、当たれとかたずをのんで見ています。

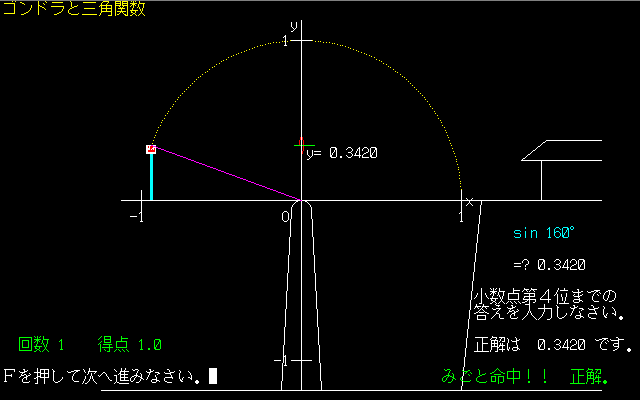
図2　ロビンフッドの矢が的に当たる

　しかし、そう簡単に当たりません。
　特に角度が 180ﾟ を越すと、ｙ座標がマイナスとなります。そのことに気付かずにプラスの値を入力している生徒のロビンフッドの矢は、的とは離れたところに突き刺さって、アウト。

　ランダムに10題出して、8題以上当たらないと、先へ進めないようになっています。
　間違ってもかまいません。あ、こうしたら的に当たるのか、結局 0ﾟから 90ﾟまでの円周上の点に引き比べればいい、と気付いてくれるのを待ちます。
　自分で見つけて会得したほうがずっと定着力があります。

　30分ぐらいたつと、半分ぐらいの生徒が正弦値の練習をクリアします。

　今度は余弦値の練習です。
　余弦値には、レスキュー隊を出動させます。
ランダムな角度が算出され、たとえば
　　　　cos 160ﾟ＝？
と問題が出ます。

　生徒たちはまだよくつかめていませんから、
　cos 20ﾟ＝ 0.9397　か cos 70ﾟ＝ 0.3420
のどちらかを入力する生徒がほとんどです。

　すると、右側からネットを持った２人のレスキュー隊が出てきて、x=0.9848 か x=0.1736 の位置に来て待ちかまえます。

　さあ、ゴンドラに乗り込んで、回り始めます。
　160ﾟ ですから、ずーっと回りだして、第２象限まで来てしまいます。
　そして160ﾟの円周上の点でストップ。ゴンドラから黄色の四角い荷物が落ちてきます。
　もちろん下にはレスキュー隊はいませんから荷物は地面に激突。
　「ガチャーン。失敗しました。」と表示が出て、やり直しです。

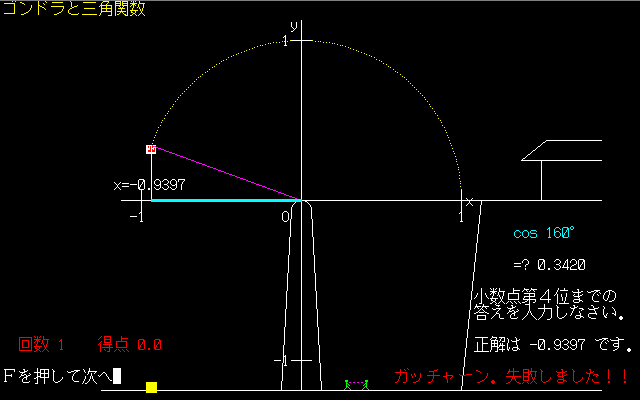
図3　レスキュー隊出動、あっ、失敗

　これを繰り返しますと、くやしいですから、なんとか成功したいと知恵をしぼります。
　どうも第２象限だと余弦値はマイナスになるようだ。第１象限に点対称かｙ軸対象で持ってくればよい、と気付きます。

　すなわち
　　　　cos θ＝ −cos(180ﾟ-θ）
の公式を感覚的につかんでいきます。

　そういったルールをみつけようとしないものはいつまでも間違います。
　それはそれでいいのです。
　となりの生徒は、なにかルールをみつけてさっさっとレスキュー隊が救い出している。自分は失敗ばかり。聞くのもしゃくだし、くやしそうです。

　「あした今日のことをまとめます。できなかった人、くやしいだろうけど、そのとき謎解きするから待って。」と授業を終わります。

　帰り際、「先生、くやしい。」「コサインまで行ったよ。」とか口々に言って帰ります。

　翌25日は、黒板授業です。

　「鈍角の三角比」と主題を書いて、
　　　　sin 120ﾟ＝？
と書きます。

　「ゴンドラがあって・・」と黒板に、円を書いて、「ぐるーっと回って・・」と円周上をチョークがなぞると、たぶん生徒の目には、ゴンドラが動いているように見えていると確信できます。

　半径１の単位円で鋭角の正弦値を定義すると、ｙ座標と同一であること、鈍角でも ｙ／ｒ の値を正弦値と定義したとき、単位円なら正弦値がｙ座標と一致することを説明します。

　「だから　sin 120ﾟ＝ sin 60ﾟ　となります。ほらこんなふうに、120ﾟのゴンドラの高さと60ﾟのゴンドラの高さは同じですから。」

　ついでに
　　　　sin 240ﾟ＝ - sin 60ﾟ
であることも説明してしまいます。

　さらに、すばやくやれた人の見つけたルールが

　　　　sin（180ﾟ-θ）＝ sin θ
　　　　sin (-θ)＝ − sinθ

であることを話して、教科書の公式と結びつけておきます。

　余弦についてもかなり容易に説明できます。
　円周上の ｘ座標が余弦値そのものであることさえ伝えれば、第２・３象限では、余弦値がマイナスになることを納得させられます。

　たった１時間のＣＡＩ授業ですが、コンピュータ画面のイメージが印象深ければ、無機質の黒板の円が、回るゴンドラに見えてしまいます。

　非日常の世界へ連れていく１時間の授業。
　本当はどの生徒も、分かりたいと願っているはずです。それに答えたい。

　「パンを食べたがっているのに、教師は石を与えている。」とわたしたちにきびしく迫られた故林竹二先生（元宮城教育大学学長）に、少しでもお返し出来るものになっているだろうかと思います。